Dynamic Programming Example with Go
Master dynamic programming by solving problems with stored solutions to avoid redundant calculations and improve efficiency at rrtutors.com Check it out!
When creating a program, the program must have an algorithm that is effective and efficient. One of the most used algorithm is dynamic programming.
What is Dynamic Programming ?
Dynamic programming is a procedure to solve a problem by storing the solution from the problem that already solved. Basically, if there is a same problem or the problem is solved before then return the stored solution rather than solving it again from scratch.
One of the problem that commonly solved using dynamic programming is fibonacci number calculation. Fibonacci number is a number that comes from a sum of two previous numbers.
0, 1, 1, 2, 3, 5, 8,... |
This is the example of solving fibonacci number using recursive approach
func fibonacci(n int) int { if n <= 2 { return 1 } else { return fibonacci(n-1) + fibonacci(n-2) } } |
Based on the code above, the base case from that function is if the value from n less than or equals 2 then the return value is 1. The recursive case is call the fibonacci() function to sum two previous numbers.
The calculation of fibonacci number with n equals 5 is performed.
func main() {
fmt.Println(fibonacci(5))
}
|
Output
5
The recursive solution of fibonacci number is illustrated in this picture.
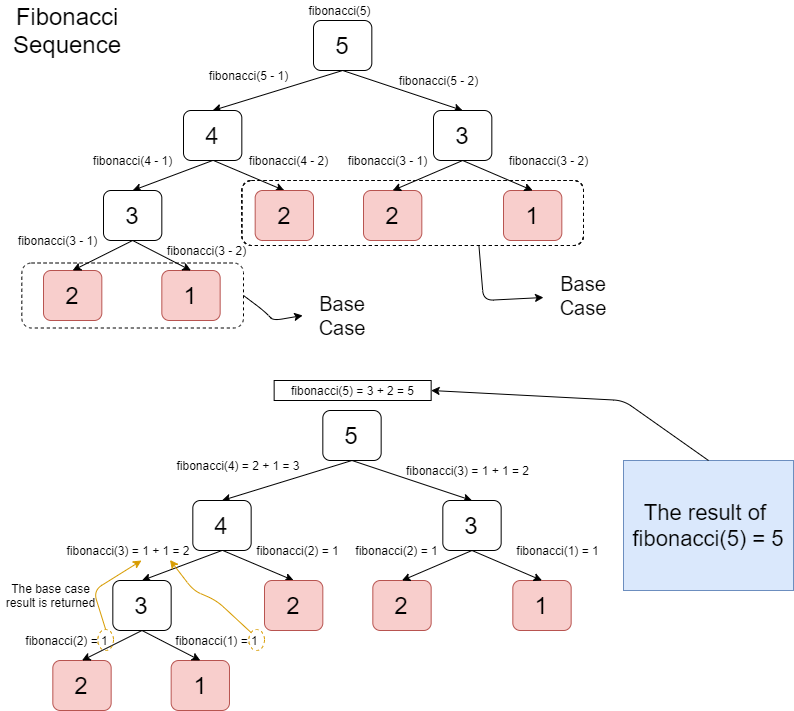
Based on the code above, the fibonacci() function works perfectly but if the fibonacci() is used with big number input, then the calculation process will really slow and could cause stack overflow exception. Stack overflow exception is an exception that is occurred because the call stack for the function is not enough to store another function call.
Dynamic Programming with Memoization
Another way to solve the fibonacci number problem is using dynamic programming by store the fibonacci calculation result that already performed in a memo. This approach is called memoization.
// create a memo var memo map[int]int = map[int]int{} func fibonacci(n int) int { // if the calculation result of "n" number exists in memo // return the calculation result from memo _, ok := memo[n] if ok { return memo[n] } if n <= 2 { return 1 } else { // store the calculation result to memo memo[n] = fibonacci(n-1) + fibonacci(n-2) return memo[n] } } |
The fibonacci function is used for two inputs
func main() {
fmt.Println(fibonacci(5))
fmt.Println(fibonacci(50))
}
|
Output
5
12586269025
Based on the code above, the function worked perfectly for small and even large input. The memoization approach of fibonacci number is illustrated in this picture.
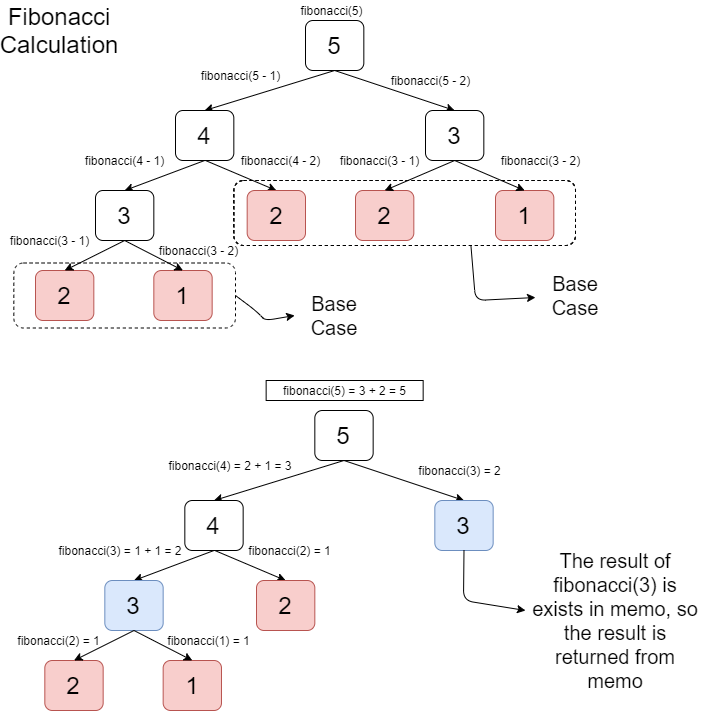
Dynamic Programming with Tabulation
Another approach to solve with dynamic programming is using table that solved iteratively.
func fibonacci(n int) int { var result []int = make([]int, n+2) result[1] = 1 for i := 0; i <= n-1; i++ { result[i+1] += result[i] result[i+2] += result[i] } return result[n] } |
The fibonacci function is used for two inputs.
func main() {
fmt.Println(fibonacci(5))
fmt.Println(fibonacci(50))
}
|
Output
5
12586269025
Based on the code above, the fibonacci function still works perfectly with tabulation approach. The illustration of using tabulation apporach can be seen in this picture.

I hope this article is helpful to learn dynamic programming using Go programming language.